第一篇数据结构
数组和链表
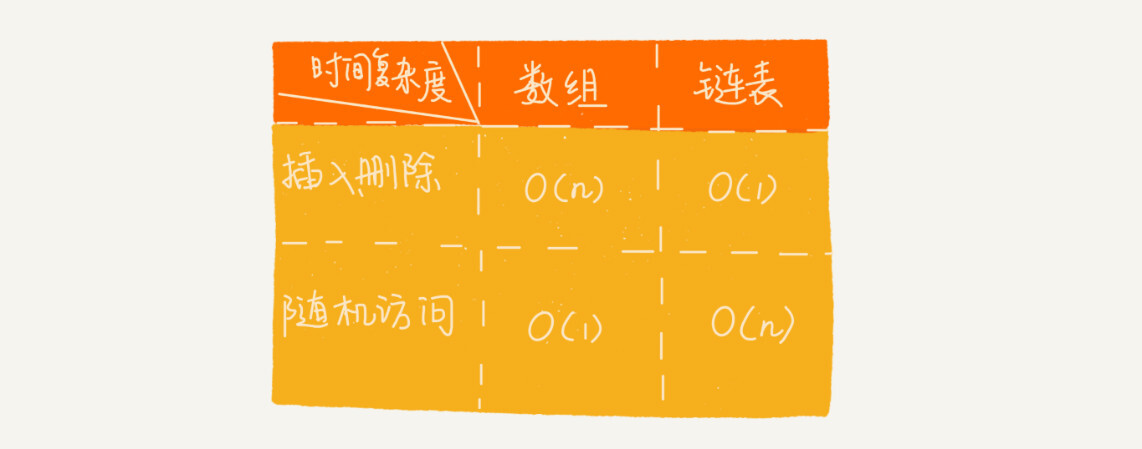
思考题: 1.如何分别用链表和数组实现LRU缓冲淘汰策略?
1)什么是缓存?
- 缓存是一种提高数据读取性能的技术,在硬件设计、软件开发中都有着非广泛的应用,比如常见的CPU缓存、数据库缓存、浏览器缓存等等。
什么是C CPU在从内存读取数据的时候,会先把读取到的数据加载到CPU的缓存中。而CPU每次从内存读取数据并不是只读取那个特定要访问的地址,而是读取一个数据块(这个大小我不太确定。。)并保存到CPU缓存中,然后下次访问内存数据的时候就会先从CPU缓存开始查找,如果找到就不需要再从内存中取。这样就实现了比内存访问速度更快的机制,也就是CPU缓存存在的意义:为了弥补内存访问速度过慢与CPU执行速度快之间的差异而引入。
2)为什么使用缓存?即缓存的特点
- 缓存的大小是有限的,当缓存被用满时,哪些数据应该被清理出去,哪些数据应该被保留?就需要用到缓存淘汰策略。
3)什么是缓存淘汰策略?
- 指的是当缓存被用满时清理数据的优先顺序。
4)有哪些缓存淘汰策略?
- 先进先出策略FIFO(First In,First Out)
- 最少使用策略LFU(Least Frenquently Used)
- 最近最少使用策略LRU(Least Recently Used)。
5)链表实现LRU缓存淘汰策略
我们维护一个有序单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,我们从链表头开始顺序遍历链表。
- 如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
- 如果此数据没有在缓存链表中,又可以分为两种情况:
- 如果此时缓存未满,则将此结点直接插入到链表的头部;
- 如果此时缓存已满,则链表尾结点删除,将新的数据结点插入链表的头部。
6)数组实现LRU缓存淘汰策略
方式一
- 首位置保存最新访问数据,末尾位置优先清理
- 当访问的数据未存在于缓存的数组中时,直接将数据插入数组第一个元素位置,此时数组所有元素需要向后移动1个位置,时间复杂度为O(n);
- 当访问的数据存在于缓存的数组中时,查找到数据并将其插入数组的第一个位置,此时亦需移动数组元素,时间复杂度为O(n)。
- 缓存用满时,则清理掉末尾的数据,时间复杂度为O(1)。
方式二
首位置优先清理,末尾位置保存最新访问数据
当访问的数据未存在于缓存的数组中时,直接将数据添加进数组作为当前最有一个元素时间复杂度为O(1);
当访问的数据存在于缓存的数组中时,查找到数据并将其插入当前数组最后一个元素的位置,此时亦需移动数组元素,时间复杂度为O(n)。
缓存用满时,则清理掉数组首位置的元素,且剩余数组元素需整体前移一位,时间复杂度为O(n)。(优化:清理的时候可以考虑一次性清理一定数量,从而降低清理次数,提高性能。)
2.如何通过单链表实现“判断某个字符串是否为回文字符串”?
方法一:半栈法
- 1.用快慢两个指针遍历,同时用栈copy慢指针指向的data。
- 2.完成后,慢指针指向中间节点,耗时为N/2.
- 3.最后用pop栈中的data和慢指针指向的data比较,耗时也是N/2.
- 所以时间复杂度为:O(N),空间复杂度因栈额外存储了一半的data,故为O(N/2)
方法二:全栈法
- 1)前提:字符串以单个字符的形式存储在单链表中。
- 2)遍历链表,判断字符个数是否为奇数,若为偶数,则不是。
- 3)将链表中的字符倒序存储一份在另一个链表中。
- 4)同步遍历2个链表,比较对应的字符是否相等,若相等,则是回文字串,否则,不是。
方法三:硬干法
- 一个指针从头取data,另一个指针遍历到底取data,比较二者
- 2.删除尾部节点,重复1.
- 时间复杂度高达 O(N^2),空间复杂度却最低O(1)