KM的博客.

算法基础

算法
字数统计: 5.3k阅读时长: 24 min
2019/06/22

算法基础

为什么要学习算法？

  • 算法是内功，决定你武功的高度

  • 算法能让你更好更快理解一门语言系统的设计理念

  • 算法能让你触类旁通

1 、数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func merge(_ nums1: inout [Int], _ m: Int, _ nums2: [Int], _ n: Int) {
     var p1 = m - 1, p2 = n - 1
     var cur = m + n - 1
     while (p2 >= 0) {
         if (p1 >= 0 && nums1[p1] >= nums2[p2]) {
             nums1[cur] = nums1[p1]
             cur -= 1; p1 -= 1
         } else {
             nums1[cur] = nums2[p2]
             cur -= 1; p2 -= 2
         }
     }
 }

面试题 16.16. 部分排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func subSort(_ array: [Int]) -> [Int] {
        //1 从左往右扫描，应该越来越大，出现比max小的，记录下来
        //2 从右往左扫描，应该越来越小，出现比min小的，记录下来
        //临界条件（array.count < 2）
        if array.count < 2 {
            return [-1, -1]
        }
        var max = array[0], R = -1
        for i in 0..<array.count {
            let v = array[i]
            if v >= max {
                max = v
            } else {
                R = i
            }
        }
  			//如果有序
         if R == -1 { return [-1, -1] }

        var min = array[array.count - 1], L = -1
        for i in (0...(array.count - 2)).reversed() {
            let v = array[i]
            if v <= min {
                min = v
            } else {
                L = i
            }
        }
        return [L, R]

    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/*
 75. 颜色分类
 给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

 此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

 注意:
 不能使用代码库中的排序函数来解决这道题。
 */
func setColors(_ nums: inout [Int]) {
    //1、遇到0 和 left交换，left++ cur++
    //2、遇到1 cur++
    //3、遇到2 和 right交换，right-- cur++  :更正交换后right--但是cur不能++，因为right的位置需要重新判断
    //循环条件cur<=right
    var cur = 0, left = 0, right = nums.count - 1
    while cur <= right {
        let curNum = nums[cur]
        if curNum == 0 {
            swapNum(&nums, cur, left)
            cur += 1
            left += 1
        } else if curNum == 1 {
            cur += 1
        } else {
            swapNum(&nums, cur, right)
            //注意：遇到2和right交换值以后，right--需要重新判断cur的值，所以cur不能++
            //cur += 1
            right -= 1
        }
    }

}
func swapNum(_ nums: inout [Int], _ i: Int, _ j: Int) {
    let temp = nums[i]
    nums[i] = nums[j]
    nums[j] = temp
}

2、链表

1
2
3
4
5
6
7
8
9
10
public class ListNode {

int val;

ListNode next;

ListNode(int x) { val = x; }

}

1： 删除链表中的节点

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {

public void deleteNode(ListNode node) {

node.val = node.next.val;

node.next = node.next.next;

}

}

2：反转链表

题目描述：反转一个单链表。

Solution1: 递归法

链表翻转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public ListNode reverseList(ListNode head) {

      if(head == null) return head;

      if(head.next == null) return head;

      ListNode newHead = reverseList(head.next);

      head.next.next = head;

      head.next = null;

      return newHead;

}

Solotion2: 非递归-双指针（https://leetcode-cn.com/problems/reverse-linked-list/solution/fan-zhuan-lian-biao-shuang-zhi-zhen-di-gui-yao-mo-/）

正确示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public ListNode reverseList(ListNode head) {

if(head == null) return head;

if(head.next == null) return head;

ListNode newHead = null;

while (head != null) {

ListNode temp = head.next;

head.next = newHead;

newHead = head;

head = temp;

}

return newHead;

}

3：反转链表 II

题目描述：反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。

说明:

1 ≤ m ≤ n ≤ 链表长度。

4：环形链表

第一步：找到快慢指针相遇的节点，如果找不到，证明没有环，返回null

第二步：head节出发与slow节点出发，相遇的节点为环的入口节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public boolean hasCycle(ListNode head) {

if (head == null || head.next == null) { return false; }

ListNode fast = head.next;

ListNode slow = head;

while (fast.next != null && fast.next.next != null) {

slow = slow.next;

fast = fast.next.next;

if (fast == slow) {

return true;

}

}

return fast == slow;

}

5：环形链表II-寻找环的入口节点

问题描述：给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

官方解读Gif

环形链表入口

6：703. 数据流中的第K大元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public class KthLargest {

private PriorityQueue<Integer> queue;

private int limit;

public KthLargest(int k, int[] nums) {

limit = k;

queue = new PriorityQueue<>(k);

for (int num : nums) {

add(num);

}

}

public int add(int val) {

if (queue.size() < limit) {

queue.add(val);

} else if (val > queue.peek()) {

queue.poll();

queue.add(val);

}

return queue.peek();

}

}



3、栈和队列

20. 有效的括号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func isValid(_ s: String) -> Bool {

var stack: [String] = []

let dic: [String: String] = [")": "(", "}": "{", "]": "["]

for c in s {

let key = String(c)

if !dic.keys.contains(key) {

stack.append(key)

} else if stack.count == 0 || dic[key] != stack.removeLast() {

return false

}

}

return stack.count == 0

}



232. 用栈实现队列

225. 用队列实现栈

4、优先队列

  1. Heap (Binary, Binomial, Fibonacci)

  2. Binary Search Tree

Mini Heap

Max Heap

Heap Wiki

• https://en.wikipedia.org/wiki/Heap_(data_structure)

239、滑动窗口最大值

5、哈希表 与双指针法

1. 两数之和

1.1暴力循环

1.2一次哈希思路
标签：哈希映射

  • 这道题本身如果通过暴力遍历的话也是很容易解决的，时间复杂度在 O(n2)
  • 由于哈希查找的时间复杂度为 O(1)，所以可以利用哈希容器 map 降低时间复杂度
  • 遍历数组 nums，i 为当前下标，每个值都判断map中是否存在 target-nums[i] 的 key 值
  • 如果存在则找到了两个值，如果不存在则将当前的 (nums[i],i) 存入 map 中，继续遍历直到找到为止
  • 如果最终都没有结果则抛出异常
  • 时间复杂度：O(n)

15. 三数之和 (硅谷面试)

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

解题思路：

  • 1、可以三重loops循环时间复杂度是O(n3)
  • 2、可以两层循环得到a+b,然后在Set集合中查找符合-(a+b)的值是否存在，时间复杂度是O(n2)
  • 3、先排序 后查找：时间复杂度为O(n2)，先排序后得到元素a, 元素b从数组下标1开始，元素c从数组下标array.length开始，检查（a + b + c）的值：
    • 如果（a + b + c）> 0, c–
    • 如果 （a + b + c）< 0, b++
    • 如果（a + b + c） == 0， 得到结果
    • 整个过程时间复杂度是O(N * N)

解题思路3 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
    public static List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> ans = new ArrayList();
        int len = nums.length;
        if(nums == null || len < 3) return ans;
        Arrays.sort(nums); // 排序
        for (int i = 0; i < len ; i++) {
            if(nums[i] > 0) break; // 如果当前数字大于0，则三数之和一定大于0，所以结束循环
            if(i > 0 && nums[i] == nums[i-1]) continue; // 去重
            int L = i+1;
            int R = len-1;
            while(L < R){
                int sum = nums[i] + nums[L] + nums[R];
                if(sum == 0){
                    ans.add(Arrays.asList(nums[i],nums[L],nums[R]));
                    while (L<R && nums[L] == nums[L+1]) L++; // 去重
                    while (L<R && nums[R] == nums[R-1]) R--; // 去重
                    L++;
                    R--;
                }
                else if (sum < 0) L++;
                else if (sum > 0) R--;
            }
        }        
        return ans;
    }

作者：guanpengchn
链接：https://leetcode-cn.com/problems/3sum/solution/hua-jie-suan-fa-15-san-shu-zhi-he-by-guanpengchn/



求最小公倍数LCM

GCD：最大公约数(Greatest Common Divisor)。指两个或多个整数共有约数中最大的一个。

LCM：最小公倍数(Least Common Multiple)。两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。

最小公倍数与最大公约数的关系：** 

1
2
3
LCM(A,B)×GCD(A,B)=A×B


其中LCM是最小公倍数，GCD是最大公约数。

1
2
3
4
5
6
7
8
//MARK:求最小公倍数 
func lcm(_ a:Int,_ b:Int) -> Int {
  //求最大公约数    
  let num:Int = gcd(a,b)
  return a * b / num
}


所以求最小公倍数的问题可以转化为求最大公约数。

18. 四数之和

拓展：K数之和

242、有效的字母异位词

6、二叉树

10道常见题目

DFS与BFS概念

  • DFS 深度优先搜索：以深度为优先级，从根节点开始一直到达叶子结点，再返回根到达另一个分支。可以细分为先序遍历，中序遍历和后序遍历。

  • BFS 广度优先搜索：按照高度顺序一层一层地访问，高层的结点会比低层的结点先被访问到。相当于层次遍历。

递归法

1、前序遍历

前序遍历递归法：左子树-根节点-右子树

1
2
3
4
5
6
7
8
9
10
11
12
13
func preorderTraversal(_ root: TreeNode?) -> [Int] {
    guard let root = root else { return[]}

    var res: [Int] = []
    res.append(root.val)
    res += preorderTraversal(root.left)
    res += preorderTraversal(root.right)

    return res

}


2、中序遍历

中序遍历递归法：左子树-根节点-右子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func inorderTraversal(_ root: TreeNode?) -> [Int] {
        guard let root = root else  { 
            return []
        }
        var res: [Int] = []
        res += inorderTraversal(root.left)
        res.append(root.val)
        res += inorderTraversal(root.right)
        
        return res
}



3、后序遍历

后序遍历递归法：左子树-右子树-根节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func postorderTraversal(_ root: TreeNode?) -> [Int] {
    guard let root = root else { return [] }
    var result: [Int] = []
    if let left = root.left {
        result += postorderTraversal(left)
    }
    if let right = root.right {
        result += postorderTraversal(right)
    }
    result.append(root.val)
    return result
}


4.1、二叉树的层次遍历

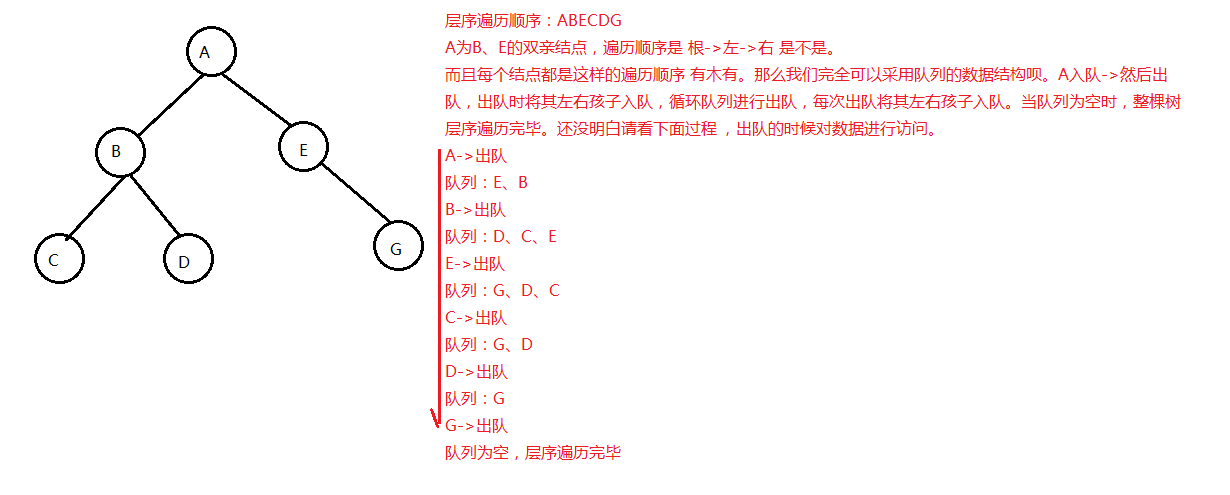
该图是借用的网上的，侵权删

图片来自网络，侵权删

实现思路：使用队列
1.将根节点入队
2.循环执行以下操作，直到队列为空

  • 将队头节点A出队，进行访问
  • 将A的左子节点入队
  • 将A的右子节点入队
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func levelOrder(_ root: TreeNode?) -> [[Int]] {
      guard let root = root else { return []}
      var result: [[Int]] = []
      var queue: [TreeNode] = []
      queue.append(root)
      while !queue.isEmpty {
          //创建存储当前level的数组
          var level: [Int] = []
          for _ in 0..<queue.count {
              //remove队列头结点，并且把该头结点的left和right加入到队列中，循环到队列为空
              let node = queue.removeFirst()
              level.append(node.val)
              if let left = node.left { queue.append(left) }
              if let right = node.right { queue.append(right)}
          }
          result.append(level)

      }

      return result
}


4.2、二叉树的层次遍历 II

从下到上依次返回每一层的结果，解决方案依然是使用队列的先进先出，node入队列的通知，node的左子树、右子树依次入队列，然后用一个temp数组来保存每一层的数值，插入到结果results数组下标位置为0的位置。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func levelOrderBottom(_ root: TreeNode?) -> [[Int]] {
    guard let root = root else { return [] }
    var results: [[Int]] = []
    var queue: [TreeNode] = [root]
    while !queue.isEmpty {
        var levelItems: [Int] = []
        for _ in 0..<queue.count {
            let node = queue.removeFirst()
            levelItems.append(node.val)
            if let left = node.left { queue.append(left) }
            if let right = node.right { queue.append(right) }
        }
        results.insert(levelItems, at: 0)
    }
    return results
}


自底向上返回层次遍历的值与普通的层次遍历的唯一区别在于每一层的结果levelItems是插入到数组下标为0的位置上，利用swift中数组插入方法insert(levelItems,at: 0)即可。

4.2、迭代法解决前中后序

递归和非递归的区别，无非是一个人为保存现场，一个代码底层自动保存现场。

前序遍历迭代法

  • 利用栈实现
    1.将root入栈
    2.循环执行以下操作，直到栈为空
    • 弹出栈顶节点top，进行访问
    • 将top.right入栈
    • 将top.left入栈

中序遍历迭代法

利用栈实现
1.设置node=root
2.循环执行以下操作
✓如果node!=null
✓将node入栈
✓设置node=node.left
✓如果node==null
✓如果栈为空，结束遍历
✓如果栈不为空，弹出栈顶元素并赋值给node

​ ➢对node进行访问
​ ➢设置node=node.right

后序遍历迭代法

◼利用栈实现
1.将root入栈
2.循环执行以下操作，直到栈为空

  • 如果栈顶节点是叶子节点或者上一次访问的节点是栈顶节点的子节点

    ✓弹出栈顶节点，进行访问

    否则
    ✓将栈顶节点的right、left按顺序入栈

5、 二叉树的最大深度

首先要明白什么是最大深度：二叉树最大深度是指根节点到最远的叶子节点最长路径上的节点数目

解法一：要求二叉树的最大深度按照递归思想也就是求max(leftHeight, rightHeight) + 1

1
2
3
4
5
6
7
8
9
10
11
12
//1、递归法：max(leftHeight, rightHeight) + 1
func maxDepth(_ root: TreeNode?) -> Int {
    if let root = root {
        var leftHeight = 0, rightHeight = 0
        if let left = root.left { leftHeight = maxDepth(left) }
        if let right = root.right { rightHeight = maxDepth(right) }
        return max(leftHeight, rightHeight) + 1
    }
    return 0
}


解放二：使用队列，分层遍历DFS，记录层数即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//2、利用队列-和分层遍历类似
//只不过分层遍历是头结点出队列时，将头队列的值保存起来，这里求最大深度是depth += 1
func maxDepth(_ root: TreeNode?) -> Int {
guard let root = root else { return 0 }
var depth = 0
var queue: [TreeNode] = [root]
while !queue.isEmpty {
    depth += 1
    let size = queue.count
    for _ in 0..<size {
        let node = queue.removeFirst()
        if let left = node.left { queue.append(left) }
        if let right = node.right { queue.append(right) }
    }
}
return depth


6、 二叉树最大宽度

解题思路：求二叉树最大宽度，可以使用分层遍历

  • 使用队列queue来记录每一层入队的结点current

  • 使用数组list来记录当前层所有结点的索引index

    • 将current的左节点入队列同时将其左孩子结点的索引 2 * index放到list中记录
    • 同理current的右孩子结点right入队列queue的同时将右结点索引2 * index + 1放到list数组中记录，这样每一层的索引都被list数组记录

  • 最后用maxLen记录当前层最大深度= list.last! - list.first! + 1

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func widthOfBinaryTree(_ root: TreeNode?) -> Int {
        guard let root = root else { return 0}
        var queue: [TreeNode] = [root]
        var list: [Int] = [1]
        var maxLen = 1
        while !queue.isEmpty {
            let size = queue.count
            for _ in 0..<size {
                let node = queue.removeFirst()
                let index = list.removeFirst()
                if let left = node.left { 
                    queue.append(left)
                    list.append(2 &* index)
                }
                if let right = node.right {
                    queue.append(right)
                    list.append(2 &* index &+ 1)
                }
            }
            if list.count >= 2 { //注意临界条件是大于等于2，因为count为1宽度也是1
                maxLen = max(maxLen, list.last! &- list.first! &+ 1)
            }
        }
    return maxLen
}

作者：mingriweiji-github
链接：https://leetcode-cn.com/problems/maximum-width-of-binary-tree/solution/fen-ceng-bian-li-shi-yong-dui-lie-qlai-ji-lu-mei-y/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。


代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
guard let root = root else { return 0 }
    var queue: [(TreeNode, Int)] = []
    queue.append((root, 1))
    var maxLen = 1
    while !queue.isEmpty {
        let count = queue.count
        for _ in 0 ..< count {
            let curr = queue.removeFirst() 
            let index = curr.1
            if let left = curr.0.left {
                queue.append((left, index &* 2))
            }

            if let right = curr.0.right {
                queue.append((right, index &* 2 + 1))
            }
        }
        if !queue.isEmpty {
            maxLen = max(maxLen, queue.last!.1 &- queue.first!.1 &+ 1)                
        }
    }

    return maxLen
}


7、 验证二叉搜索树

1、递归法

递归法解题的关键在于：maxLeft < root.val < minRight

  • 1、临界条件:root==null
  • 2、递归左子树，找到最大值max和根节点root.val进行比较，如果左子树的max大于等于根节点的值，返回false
  • 3、递归右子树，找到右子树的最小值min和根节点root.val比较，如果右子树的min小于等于根节点，返回false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public boolean helper(TreeNode root, Integer min, Integer max) {
       if (root == null) return true;

       if (min != null && min > root.val) return false;
       if (max != null && max < root.val) return true;

       return helper(root.left,min,root.val) && helper(root.right,root.val,max);
       
   }
   public boolean isValidBST(TreeNode root) {
       return helper(root,null,null);
   }



上面的help()方法不能通过测试用例[1,1]这种重复元素的数组，判断条件错误，修改如下：

Java版本

1
2
3
4
5
6
7
8
9
10
11
public boolean helper(TreeNode root, Integer min, Integer max) {
        if (root == null) return true;

        if (min != null && min >= root.val) return false;
        if (max != null && max <= root.val) return true;

        return helper(root.left,root.val,max) && helper(root.right,min,root.val);
        
}


swift版本:注意可选项解包，和判断条件是left.max >= root.val, right.min <= root.val

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func isValidBST(_ root: TreeNode?) -> Bool {
      guard let root = root else { return true }
      return helper(root,nil,nil)
  }

  func helper(_ root: TreeNode?, _ min: Int?, _ max: Int?) -> Bool {
      guard let root = root else { return true }

    //左节点需要小于根节点值
      if let min = min,
      min <= root.val {
          return false
      }
    //右节点需要大于根节点
      if let max = max,
      max >= root.val {
          return false
      }
      return helper(root.left, root.val,max) && helper(root.right, min, root.val)
  }


8、对称二叉树

解题思路：给定一个二叉树，看它是否镜像对称关键是1、左右子树的值相等 2、左子树的left和右子树的right是镜像对称，利用递归思想容易解决。

24ms代码实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func isSymmetric(_ root: TreeNode?) -> Bool {
    return isMirror(root,root)
}
func isMirror(_ p: TreeNode?, _ q: TreeNode?) -> Bool{
    //注意临界条件判断，先判断p、q均为空的情况
    if p == nil && q == nil {
        return true
    }
    if p == nil || q == nil {
        return false
    }         
    return (p!.val == q!.val) && isMirror(p!.left, q!.right) && isMirror(p!.right, q!.left)
}


20ms代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func isSymmetric(_ root: TreeNode?) -> Bool {
     guard let root = root else { return true }
     return isMirror(root.left, root.right)
 }
 func isMirror(_ p: TreeNode?, _ q: TreeNode?) -> Bool {
     if p == nil, q == nil {
         return true
     }
     if let p = p, let q = q, p.val == q.val {
         return isMirror(p.left, q.right) && isMirror(p.right, q.left)
     }
     return false
 }


第二遍：

执行用时 :16 ms, 在所有 swift 提交中击败了94.96%的用户

内存消耗 :19.9 MB, 在所有 swift 提交中击败了5.00%的用户

1
2
3
4
5
6
7
8
9
10
11
12
13
func isSymmetric(_ root: TreeNode?) -> Bool {
    guard let root = root else { return true }
    return isMirror(root.left, root.right)
}
func isMirror(_ p: TreeNode?, _ q: TreeNode?) -> Bool {
    if p == nil && q == nil { return true }
    if let p = p,let q = q, p.val == q.val {
        return isMirror(p.left, q.right) && isMirror(p.right, q.left)
    }
    return false
}


9、翻转一颗二叉树

迭代就要遍历二叉树，利用分层遍历用队列交换每个结点的左右子树。

8ms迭代法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func invertTree(_ root: TreeNode?) -> TreeNode? {
        //迭代法翻转二叉树,交换每一个结点的左右子树，我们用队列储存没有交换过的左右子树的结点，拿到current结点后，交换左右结点，然后再将该节点的左右结点加入到队列中。直到队列为空截止。
        guard let root = root else { return nil }
        var queue: [TreeNode] = [root]
        while !queue.isEmpty {
            var node = queue.removeFirst()
            let temp = node.left
            node.left = node.right
            node.right = temp
            if let left = node.left { queue.append(left) }
            if let right = node.right { queue.append(right) }
        }
        return root
    }


16ms递归法：

1
2
3
4
5
6
7
8
9
10
11
12
13
func invertTree(_ root: TreeNode?) -> TreeNode? {
        guard let root = root else { return nil }
        let temp = root.left
        root.left = root.right
        root.right = temp
        
        invertTree(root.left)
        invertTree(root.right)

        return root
    }


8ms递归法：同上面的区别是没有解包，解包耗时8ms?

1
2
3
4
5
6
7
8
9
10
11
12
13
func invertTree(_ root: TreeNode?) -> TreeNode? {
    if root == nil { return nil }
    let temp = root?.left
    root?.left = root?.right
    root?.right = temp

    invertTree(root?.left)
    invertTree(root?.right)

    return root
}


第二遍：分层遍历后不要把当前节点放入队列中，我们要的是翻转二叉树，不需要记录当前节点node

7、二叉树搜索树

10道常见题目

8、合并

21. 合并两个有序链表

递归法

1
2
3
4
5
6
7
8
9
10
11
12
13
func mergeTwoLists(_ l1: ListNode?, _ l2: ListNode?) -> ListNode? {
    if l1 == nil { return l2 }
    if l2 == nil { return l1 }
    if l1!.val < l2!.val {
        l1?.next = mergeTwoLists(l1?.next, l2)
        return l1
    } else {
        l2?.next = mergeTwoLists(l1, l2?.next)
        return l2
    }
}


迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func mergeTwoLists(_ l1: ListNode?, _ l2: ListNode?) -> ListNode? {
    var l1 = l1
    var l2 = l2
    let head = ListNode(-1)
    var cur = head
    while (l1 != nil && l2 != nil) {
        //cur.next 记录当前的head
        if l1!.val <= l2!.val {
            cur.next = l1
            l1 = l1?.next
        } else {
            cur.next = l2
            l2 = l2?.next
        }
        //cur后移
        cur = cur.next!
    }
    //处理链表为空
    cur.next = l1 == nil ? l2 : l1
    return head.next
}


原文作者：KM

原文链接：https://mingriweiji-github.github.io/2019/06/22/2020%E7%AE%97%E6%B3%95%E5%9F%BA%E7%A1%80/

发表日期：六月 22日 2019, 2:18:15 凌晨

更新日期：五月 11日 2022, 12:01:43 凌晨

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 算法基础
    1. 1.0.0.1. 为什么要学习算法？
  • 1.1. 1 、数组
    1. 1.1.0.1. 面试题 16.16. 部分排序
  • 1.2. 2、链表
    1. 1.2.0.0.1.
  • 1.2.0.1. 1： 删除链表中的节点
  • 1.2.0.2. 2：反转链表
  • 1.2.0.3. 3：反转链表 II
  • 1.2.0.4. 4：环形链表
  • 1.2.0.5. 5：环形链表II-寻找环的入口节点
  • 1.2.0.6. 6：703. 数据流中的第K大元素
  • 1.3.
  • 1.4. 3、栈和队列
    1. 1.4.0.1. 20. 有效的括号
    2. 1.4.0.2. 232. 用栈实现队列
    3. 1.4.0.3. 225. 用队列实现栈
  • 1.5. 4、优先队列
    1. 1.5.0.1. 239、滑动窗口最大值
  • 1.6. 5、哈希表 与双指针法
    1. 1.6.0.1. 1. 两数之和
    2. 1.6.0.2. 15. 三数之和 (硅谷面试)
    3. 1.6.0.3. 求最小公倍数LCM
    4. 1.6.0.4. 18. 四数之和
    5. 1.6.0.5. 拓展：K数之和
    6. 1.6.0.6. 242、有效的字母异位词
  • 1.7. 6、二叉树
    1. 1.7.0.1. 10道常见题目
  • 1.8. DFS与BFS概念
    1. 1.8.1. 递归法
      1. 1.8.1.1. 1、前序遍历
      2. 1.8.1.2. 2、中序遍历
      3. 1.8.1.3. 3、后序遍历
      4. 1.8.1.4. 4.1、二叉树的层次遍历
      5. 1.8.1.5. 4.2、二叉树的层次遍历 II
      6. 1.8.1.6. 4.2、迭代法解决前中后序
      7. 1.8.1.7. 前序遍历迭代法
      8. 1.8.1.8. 中序遍历迭代法
      9. 1.8.1.9. 后序遍历迭代法
      10. 1.8.1.10. 5、 二叉树的最大深度
      11. 1.8.1.11. 6、 二叉树最大宽度
      12. 1.8.1.12. 7、 验证二叉搜索树
      13. 1.8.1.13. 8、对称二叉树
      14. 1.8.1.14. 9、翻转一颗二叉树
  • 1.9. 7、二叉树搜索树
    1. 1.9.1. 10道常见题目
      1. 1.9.1.1. 验证二叉搜索树
      2. 1.9.1.2. 二叉搜索树中的插入操作
      3. 1.9.1.3. 二叉搜索树中的搜索
      4. 1.9.1.4. 删除二叉搜索树中的节点
      5. 1.9.1.5. 二叉搜索树的最小绝对差
      6. 1.9.1.6. 二叉搜索树结点最小距离
      7. 1.9.1.7. 将有序数组转换为二叉搜索树 *
      8. 1.9.1.8. 二叉搜索树的范围和 *
      9. 1.9.1.9. 二叉搜索树的最近公共祖先 *
      10. 1.9.1.10. 二叉搜索树中第K小的元素 **
      11. 1.9.1.11. 二叉搜索树迭代器 **
      12. 1.9.1.12. 恢复二叉搜索树
      13. 1.9.1.13. 平衡二叉树
  • 1.10. 8、合并
    1. 1.10.0.1. 21. 合并两个有序链表
    • Total : 35
    2022
    2021
    2020
    2019
    2018
    java 算法 Swift专题 iOS Flutter 开发工具 Swift book
    算法 源码 Flutter 指南 Swift 图像 逆向 book